Projet sur l'algorithme des abeilles

Résumé

Ce document reflète une étude succincte de l'algorithme des abeilles butineuses. A travers une étude d'un comportement de la nature puis de la mise en équation de ce phénomène, l'idée est de comprendre les principes de cet algorithme et de voir qu'elles sont les utilités qu'il apporte dans le cadre d'une recherche de solutions et/ou d'optimisation dans des problèmes complexes. La comparaison à d'autres algorithmes et la recherche de ses domaines d'application nous amenera à une critique de celui-ci.

Les bases de l'algorithme

Pour trouver de la nourriture, les abeilles d'une même colonie, parcourent de longues distances dans différentes directions. Une petite partie de ces abeilles cherchent continuellement de nouvelles zones de fleurs. Ces abeilles éclaireuses se rendent aléatoirement sur des lieux autour de la ruche, évaluant si les sources de nourriture rencontrées sont intéréssantes. Lorsqu'elles retournent à la ruche, ces éclaireuses déposent leur nourriture récoltée. L'abeille ayant trouvée la source la plus intéréssante se rend dans une zone de la ruche (la salle de danse) et réalise la danse frétillante. Avec cette danse, l'abeille éclaireuse communique l'endroit découvert aux autres abeilles pour exploiter la zone. L'abeille éclaireuse retourne sur le lieu afin de collecter plus de nourriture. Elle avertit ainsi de l'état de la source, et si celle-ci est profitable, les abeilles continuent de l'exploiter. Plus la zone est intéréssante, plus il y a d'abeilles recrutées. Grâce à ce procédé, les colonies d'abeilles sont capables de changer rapidement de zone de butinage se focalisant toujours sur les zones les plus intéréssantes.

Les origines

La découverte de la danse des abeilles

Au cours de la dernière décennie, les algorithmes d'abeilles, inspirés de la nature, sont devenus un outil prometteur et puissant. Les danses des abeilles ont étés décrites dès la fin du XVIIIième siècle, mais ce n'est qu'au XXième siècle que l'éthologue Karl Von Frisch (1886-1982) propose une explication rationnelle partielle. Karl Von Frisch a été longtemps professeur de zoologie à Munich. Il est considéré comme l'un des plus important éthologiste de langue allemande. Au cœur de son œuvre se trouve la recherche sur les perceptions sensorielles et les danses des abeilles, ainsi que sur les modalités de la communication entre ces animaux. Pour ses travaux, il fut distingué par le prix Nobel de physiologie ou médecine en 1973. La motivation de ce prix était « pour les découvertes concernant l'organisation et l'incitation des comportements individuels et sociaux ». Ces informations sont tirées de [7].

Les origines des algorithmes d'abeilles

Basé sur ces découvertes, ce n’est que très récemment que l’on a réussi à réaliser un algorithme en lien avec ces fameuses danses. Ces algorithmes font partie de la famille des algorithmes d’optimisation stochastique. Ils permettent de rechercher de manière globale le ”meilleur” candidat représenté par un vecteur de paramètres ou un programme. Ces algorithmes sont aussi définis comme un algorithme évolutionnaire qui s’inspire de l’observation de notre environnement. D’après la bibliographie, il semble que l'algorithme « Honey-bee » a été réalisé pour la première fois vers 2004 par Craig A.TOVEY à Georgia Tech en collaboration avec Sunil NAKRANI. Entre 2004 et 2005, Xin-She YANG à l’Université de Cambridge a développé le VBA (Virtual Bee Algorithm) pour résoudre des problèmes d’optimisation numérique. Cet algorithme permet d’optimiser à la fois les fonctions et les problèmes discrets, cependant ils n’ont donné comme exemples que les fonctions à deux paramètres. Un peu plus tard, en 2005, Haddad, Afshar et leurs collègues ont présentés un algorithme dit « Honey-Bee Mating Optimization » (HBMO) qui a ensuite été appliqué à la modélisation de réservoirs et de clustering. En 2006, B. Bastrurk et D. Jarabogo en Turquie, ont développés un algorithme appelé « Artificial Bee Colony » pour l’optimisation de fonctions numériques. Ces dernières informations proviennent de multiples ouvrages et documents cités en [2] et [11].

Les principes

Il faut savoir que l'algorithme des abeilles est considéré comme étant un algorithme de type multi agents. Un agent est une entité qui peut être vue comme percevant et agissant de façon autonome sur son environnement. On parle d'agent autonome parce que son comportement dépend au moins partiellement de son expérience. Un système multi-agents (SMA) est constitué d'un ensemble de processus informatiques se déroulant en même temps, donc de plusieurs agents vivant au même moment, partageant des ressources communes et communicant entre eux. Le point clé des systèmes multi-agents réside dans la formalisation de la coordination entre les agents. La recherche sur les agents est ainsi une recherche sur :

Dans l'algorithme des abeilles, les abeilles d'une même ruche, sont vues comme des agents. En effet, chacune d'entre elle agit seule et de façon autonome dans un but commun à savoir rechercher de la nourriture. Il existe plusieurs types d'abeilles pour réaliser l'objectif : les éclaireuses et les butineuses. Afin de communiquer entre elles, elles réalisent des danses spécifiques à l'action recherchée :

Pour expliquer le principe de cet algorithme, voici un schéma bloc présentant ses différentes étapes :

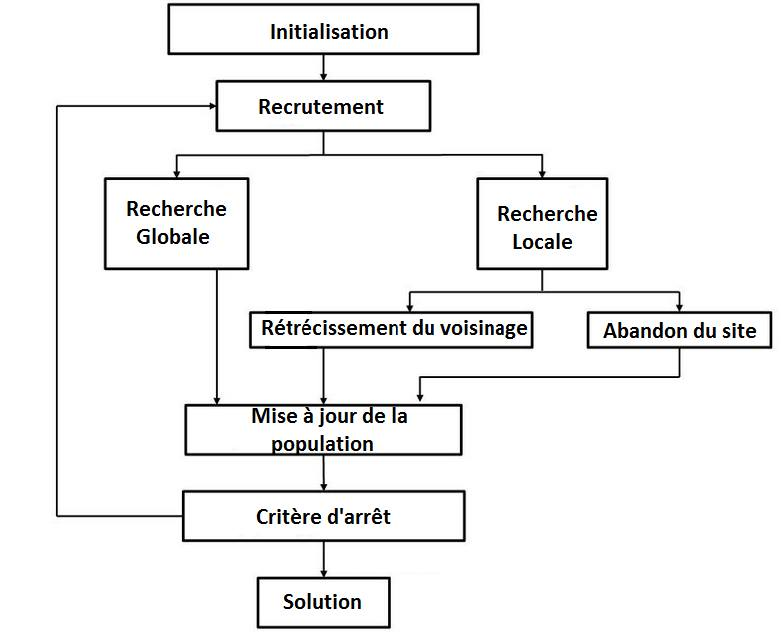
schéma bloc du principe de l'algorithme

Ces dernières informations proviennent des sources [12] et [10].

Tout d’abord nous pouvons faire les correspondances suivantes :

L'algorithme des abeilles est constitué de 6 étapes qui font l’analogie avec le fonctionnement/organisation des abeilles à la recherche d’une source de nourriture. Les voici :

Il existe 3 types d’abeilles :

Les paramètres importants :

La taille totale des colonies d'abeilles est n = ne·nre + (nb-ne).nrb + ns abeilles (sites élite butineuses + butineuses restant sur les meilleurs site + éclaireuses).

ETAPE 1 : Initialisation

En simple : N abeilles éclaireuses sont placées aléatoirement dans l'espace de recherche.

En compliqué : Elles évaluent la quantité de nectar (ou le fitness) de leur emplacement (solution possible) et pour chaque emplacement un voisinage est délimité. Chaque solution x_i (i=1,2,…,N) est initialisée par les éclaireuses, et représente un vecteur de solution au problème d’optimisation et les variables que contiennent chaque vecteur doivent ensuite être optimisées.

Les étapes qui suivent font partie d'un cycle qui est réhitéré. C=1,2,…,C_max ces cycles représentent des processus de recherches faits par les butineuses actives, inactives et les éclaireuses.

ETAPE 2 : Recrutement

En simple : Les éclaireuses qui ont visité les emplacements avec le meilleur fitness font la danse frétillante : elles recrutent ainsi des butineuses qui auront pour but de chercher dans le voisinage une solution plus prometteuse. Les éclaireuses qui ont trouvé les meilleurs emplacements/solutions lors de la phase d'initialisation recrutent plus de butineuses tandis que les autres recrutent les butineuses restantes.

En compliqué : Les solutions visitées par les éclaireuses sont classées en fonction de leurs fitness. Celles qui ont trouvé les meilleures solutions (nb : meilleurs sites) exécutent la danse frétillante. Parmi celle-ci, celles qui ont débarqué sur les ne meilleures solutions (appelé sites d'élites) recrutent NRE butineuses chacunes. Les éclaireuses restantes (nb –ne) recrutent les butineuses restantes (nrb ≤ nre chacun).

ETAPE 3 : Recherche locale

En simple : Les butineuses actives recherchent dans le voisinage (précédemment visité par les éclaireuses) de nouvelles sources. Les abeilles butineuses recrutées sont aléatoirement dispersées dans le voisinage de la source initiale. Si l'une d'elles trouve une source avec un meilleur fitness que la précédente, elle devient éclaireuse.

En compliqué : Les butineuses effectuent une recherche locale à proximité des solutions annoncées par les éclaireuses. Pour chacun des nb sites d’élites, les butineuses recrutées sont dispersées au hasard dans une hyperbox de taille s1, ... , sn = une centrée sur la solution visitée par l'éclaireuse. Dans l’algorithme des abeilles, cette hyperbox est appelée un « patch fleur». Si une butineuse atterrit sur une solution de meilleur fitness que la solution marquée par l'éclaireuse, la butineuse devient alors une éclaireuse. En revanche si elles ne trouvent pas de meilleurs source, la taille du voisinage est rétrécie (ETAPE 4).

ETAPE 4 : Rétrécissement de voisinage

Si aucune butineuse ne trouve de solution avec un meilleur fitness que celle de la source (emplacement de l’eclaireuse), la taille du patch fleurs est rétréci. Les patchs sont généralement initialisés pour couvrir une grande région de l'espace de recherche, souvent tout l'espace, et progressivement réduits. Le mécanisme de rétrécissement du voisinage vise à se concentrer progressivement sur une zone de recherche étroite autour du pic de fitness. A chaque cycle de stagnation, la taille du patch fleur est diminuée en utilisant la formule heuristique suivante : a (t + 1) = 0,8 · a (t) où a ( t) est le côté de l’hyperbox

ETAPE 5 : L'abandon du site

Si la procédure de recherche locale ne parvient pas à apporter une amélioration dans ce patch fleur, la recherche est supposée avoir trouvé l'optimum de fitness locale. Dans ce cas, le patch de fleurs est abandonné et une nouvelle abeille éclaireuse est réinitialisée à un endroit aléatoire dans l'espace de recherche.

ETAPE 6: Recherche globale

A chaque cycle de l’algorithme des abeilles, la recherche globale est effectuée par ns - nb abeilles éclaireuses. Ces éclaireuses sont placées de manière aléatoire dans l'espace de recherche.

Mise à jour de la population

À la fin de chaque cycle d'optimisation, une nouvelle liste d’éclaireuses est crée à partir des nb éclaireuses résultantes de la procédure de recherche locale (pour chaque patch fleur, l'abeille qui a atterri sur la meilleure solution), et les ns - nb éclaireuses résultantes de la procédure de recherche globale (les abeilles dispersées au hasard).

Critère d'arrêt

L'algorithme est arrêté, soit quand une solution considérée comme acceptable a été trouvée, soit quand le nombre maximum de cycles a été atteint.

Domaines d'applications

Les applications de l'algorithme des abeilles sont nombreuses, c'est pourquoi nous avons choisi de n'en présenter que quelques une afin d'approfondir dans chaque cas son utilitée. Plus qu'un véritable outil, cet algorithme est utilisé pour optimiser les outils existant.

Fonctions d'optimisation

Dans l'article The Bees Algorithm – A Novel Tool for Complex Problems écrit par des docteurs de l'Université de Cardiff ([4]), sont présentés plusieurs problèmes d'optimisation combinatoires ou de fonctions. Des benchmarks, autrement dit des tests de comparaisons, sont réalisés entre différent algorithmes sur des fonctions mathématiques pour déterminer celui qui est le plus efficace pour répondre au problème. La tableau numero 2 (table2) du document révèle que l'algorithme des abeilles (BA - Bees Algorithm) obtient des performances supérieures aux autres algorithmes testés tels que l'algorithme génétique (GA - Genetic Algorithm) ou l'algorithme des colonies fourmies (ANTS - Ant Colony System). Sur la suite de De Jong permettant de tester l'optimisation d'algorithme, le BA trouve l'optimum (solution proche de la solution optimale) 120 fois plus rapidement que le ANTS et 207 fois plus rapidemment que celui du GA. Le point fort de cet algorithme est qu'il ne tombe pas dans le piège du point optimum local sur lequel d'autres echouent, et possède donc un ratio de 100% pour trouver l'optimum.

Le BA pour résoudre le problème du voyageur de commerce

Le BA aussi appelé BCO (Bee Colony Optimization) est utlilisé dans le problème du TSP (Traveling Salesman Problem [8]) dit problème du voyageur de commerce en français. Ce problème mathématique consiste à trouver le chemin le plus court pour visiter toutes les villes d'une zone donnée en passant qu'une seule fois par ville et en revenant au point de départ une fois toutes les villes visitées. Ce problème en apparence simple devient complexe lorsque le nombre de villes est important. On parle alors de problèmes NP-complets [9] qui ne sont à ce jour non solvables dans un temps polynomial, c'est à dire qu'il n'y a pas de solution algorithmique dont le temps d'exécution est proportionnel à un polynôme fonction de ses entrées. Ainsi pour beaucoup de développeurs et informaticiens confrontés à des problèmes de type NP-complets, la solution se trouvera dans un algorithme d'opitimisation ayant pour but de s'approcher le plus rapidemment possible d'une solution optimum comme le fait l'algorithme des abeilles.

Graphiques de contrôles

Les graphiques de contrôles sont employés dans l'industrie pour la maîtrise des statistiques de procédés. Ils permettent la rectification éventuelle d'un problème sur la chaîne de production. L'automatisation de cette technique se veut de détecter les anomalies sur le système en place via des algorithmes de reconnaissance de patterns. Dans l'article Chart Pattern Recognition using the Bees Algorithm publié par M. Ghanbarzadeh Afshin ([1]), l'auteur démontre que le BA appliqué au réseau dit de RBF (Radial Basis Function) permettant de trouver l'erreur entre le pattern testé et le pattern voulu, diminue la marge d'erreur. Il optimise donc, avec un choix de paramètres précis, la détection d'erreurs.

La classification des bois défectueux

La classification des bois défectueux fait parti des problèmes complexes difficilement solvables par soucis d'optimisation. Là encore, l'intérêt pour les algorithmes dits intelligents est grand puisqu'ils permettent de trouver des solutions proches de la solution exacte dans un temps relativement court. En particulier, l'algorithme des abeilles qui est appliqué comme solution au problème de l'identification des défaults dans les bois aglomérés. C'est sur la qualité de ce bois que se joue celle du bois aggloméré lorsque les planches sont colées pour le former. C'est en réalité le SVM (Support Vector Machine) network qui permet de détecter ces defaults. Le rôle du SVM est de trouver l'hyperplan optimal qui classera chaque pattern dans la classe à laquelle il appartient ([6]). Un autre article de l'Université de Cardiff, Using the Bees Algorithm to Optimise a Support Vector Machine for Wood Defect Classification ([5]), explique que dans la procédure initiale de la technique SVM utilisée pour la classification des bois défectueux, l'algorithme des abeilles intervient dans l'optimisation de deux paramètres γ et C. Le premier représente la précision de la classification tandis que le second représente le facteur de poids image du compromis entre une incertitude dans la classification de certains points. L'expérience réalisée met en place une comparaison de la précision dans la classification entre un SVM standard et un SVM optimisé (par le BA). Le résultat révèle que l'optimisation du BA permet une augmentation de la moyenne de la précision de la classification de 82.42% à 88.16%.

Critique de l'algorithme

Au vu des explications précédentes, on peut en déduire différents avantages et invonvénients de l'utilisation d'un algorithme de type abeille [2].

Avantages :

Inconvénients :

Références Bibliographiques