Résumé
L' algorithme génétique, comme tout algorithme bio-inspiré, se base sur une observation du vivant.
« La génétique (du grec genno γεννώ, « donner naissance ») est la science qui étudie l'hérédité et les gènes, c'est une sous-discipline de la biologie. Une de ses branches, la génétique formelle, ou mendélienne, s'intéresse à la transmission des caractères héréditaires entre des géniteurs et leur descendance. » -Wiki-
Tout comme la génétique formelle, les algorithmes génétiques s’appuient sur la transmission de parties de codes et leurs mutations afin de trouver la meilleure solution possible. Le but étant de faire évoluer une population de base vers une solution idéale par croisements successifs et mutations aléatoires pour chaque nouvelle génération de solutions.
Les algorithmes génétiques apportent une bonne solution pour un programme évoluant dans un avenir incertain voir inconnu. On pourra citer comme exemple d’utilisation un système d’esquive de missile d’avion de chasse. Ce dernier peut esquiver 99% des projectiles tous types confondus, sans même en connaitre la nature.
Néanmoins, cet algorithme est très compliqué à mettre en place : par le choix du codage, le choix de la population initiale ainsi que par l’incertitude de trouver une solution dû à la mise en jeux de deux probabilités pc et pm (probabilité de croisement et de mutation).
Analogie avec le monde de la biologie
Cette partie va permettre de comprendre d'où proviennent les notions de biologies, ici expliquées afin de comprendre ce qui à inspiré les algorithmes génétiques
Avant de parler d’algorithmes génétiques, il est essentiel de comprendre que ces algorithmes pensés par les humains et exécutés par les machines sont le fruit de longues recherches, basées sur l’observation de phénomènes microscopiques et qui sont l’essence même des espèces.
Au XIXème siècle, nous sommes aux prémices de la génétique. Si la théorie du transformisme de Lamarck ouvre la voie, c’est Charles Darwin (1809-1882) qui explicite la théorie de l’évolution dans son ouvrage « De l’Origine des espèces » (1859). Il y démontre deux grands principes : l'unité et la diversité du vivant s'expliquent par l'évolution, et le moteur de l'évolution adaptative est la sélection naturelle. Par la suite, Gregor Mendel (1822-1884) met en place les 3 lois concernant l’hérédité biologique. Ces lois, combinées avec la découverte des chromosomes et de l’ADN, notamment grâce aux travaux de Morgan et Avery dans la première moitié du XXème siècle, et ceux de Watson et Crick en 1953, sont les fondements de la génétique contemporaine et de l’évolution moléculaire.
1) Notions de génétique
Pour bien comprendre, il est essentiel de définir le terme génétique. Il s’agit de la science de l’hérédité. Elle étudie les caractères héréditaires des individus, leur transmission au fil des générations et leurs variations.
Le génome est l’ensemble du matériel génétique d’un organisme, et contient à la fois des séquences codantes (qui codent pour des protéines) et non codantes. Pour la plupart des organismes, le génome correspond à l’ADN (acide désoxyribonucléique, DNA en anglais) présent dans les cellules. Cependant pour les rétrovirus, il s’agit cependant d’ARN (assemblage de ribonucléotides possédant de très nombreuses fonctions dans la cellule).
On peut voir sur le schéma suivant une suite de zooms successifs qui nous montrent l’imbrication des constituants d’un organisme, ici un poisson.
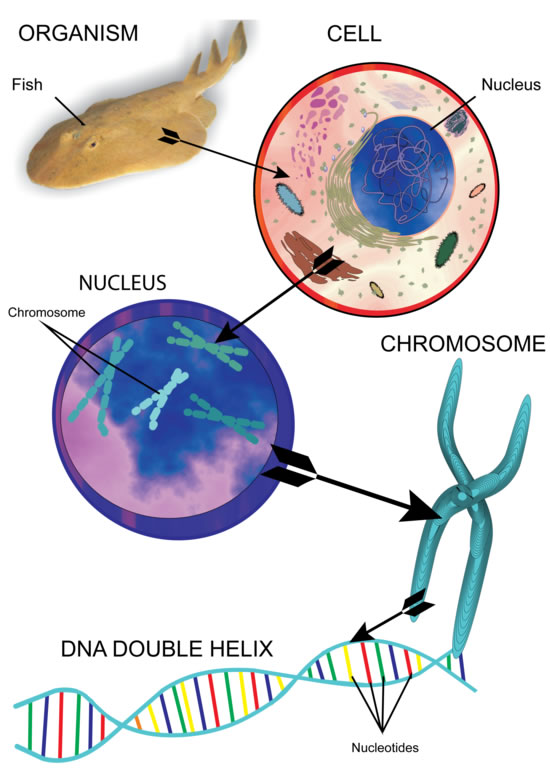
On peut comparer l’ADN avec un livre dont le langage est constitué de quatre bases azotées, appelés nucléotides : l’adénine, la cytosine, la guanine et la thymine (A, C, G et T). La manière dont les nucléotides sont agencés dans l’ADN constitue le code génétique. On peut lire ce code à l’aide d’une machinerie cellulaire. Le séquençage de l’ADN permet de connaître l’enchainement des nucléotides et de cartographier le génome. Suivant les organismes, le génome a une taille variable, de quelques milliers à plusieurs millions de paires de bases. En 1990, le projet génome humain est lancé et permet le séquençage de l’ADN humain, composé d’environs 3,4 milliards de nucléotides.
Sur le schéma précédent, on peut voir que des chromosomes sont présents dans nos cellules (23 paires pour les humains). Ils sont constitués d’ADN. Les gènes, qui sont les unités d’hérédité contrôlant un caractère particulier (par exemple la couleur des yeux), sont des segments d’ADN, situé à des endroits bien précis appelés locus, sur le chromosome. Le noyau de la cellule est donc une sorte de bibliothèque qui renferme le patrimoine héréditaire de l’individu, et dont les chromosomes sont les livres. Les gènes sont les pages de ces livres. On dénombre aujourd’hui près de 25000 gènes chez l’être humain.
Les gènes peuvent avoir différentes valeurs. Par exemple, prenons le cas du gène définissant la couleur des yeux. Il peut prendre suivant les individus plusieurs valeurs selon l’agencement des nucléotides le composant (bleu, vert, marron, ainsi que les nuances…). Ces différentes valeurs sont appelées allèles. C’est grâce à cela que tous les membres d’une espèce sont uniques.
Sources:
- Institut océanographique de Bedford-
2) Recombinaison génétique dans l’ADN
Lors de la reproduction, on observe un phénomène de recombinaisons des gènes. Voici une définition de la recombinaison génétique que l’on peut assimiler à un brassage génétique:
« Phénomène conduisant à l’apparition, dans une cellule ou dans un individu, de gènes ou de caractères héréditaires dans une association différente de celle observée chez les cellules ou individus parentaux » -Wiki-
Cette définition peut être illustrée par le schéma suivant :
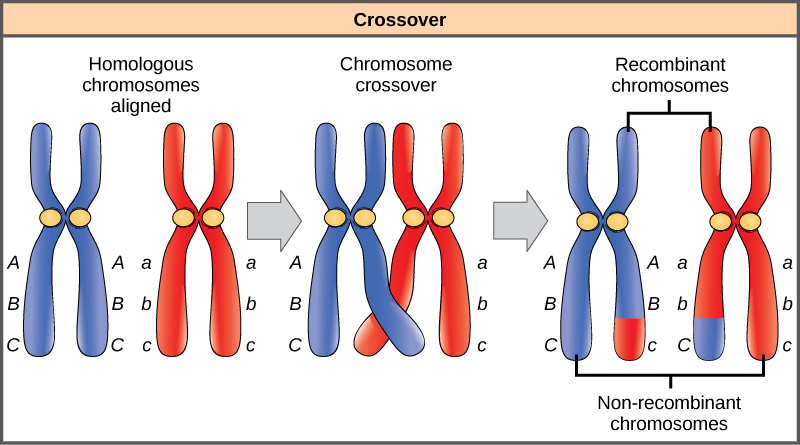
Il s’agit en réalité de recombinaison de l’ADN, c'est-à-dire les processus par lesquels les molécules d’ADN sont coupées puis jointes l’une à l’autre. En générant de nouvelles combinaisons génétiques, les recombinaisons naturelles sont un des mécanismes à l'origine de la diversité d'une population. Ce brassage génétique, facilité par la reproduction sexuée, est un des mécanismes essentiels de l'évolution des espèces.
Sources:
3) Mutation génétique dans l’ADN
Voici une définition de la mutation génétique :
« Une mutation est une modification de l'information génétique dans le génome d'une cellule ou d'un virus. C'est donc une modification de la séquence de l'ADN, ou de l’ARN » -Wiki-
Pour la comprendre, remontons un siècle en arrière. La drosophile, une mouche dont les générations sont courtes et possédant 4 chromosomes géants, va servir la science et permettre la découverte des mutations. En 1910, Morgan découvre que, après avoir subit des radiations, des mouches aux yeux normalement rouges donnent naissances à des mouches aux yeux blancs, ou encore possédant une paire d’ailes supplémentaire. Il nomme ces transformations des mutations. A ce moment, les mécanismes internes de la génétique ne sont pas encore connus, mais il comprend alors que ces caractères spécifiques sont liés à des petites parcelles de chromosomes, les gènes. Vous pouvez observer des drosophiles mutantes sur l’image suivante.

Actuellement, ce phénomène participant à l’évolution est bien connu, et on distingue plusieurs types de mutations, que nous ne détaillerons pas dans ce document : les mutations ponctuelles, chromosomiques, dynamiques, et somatiques (ou germinales). Les mutations sont aléatoires, mais leur probabilité est augmentée par des mutagènes, qui peuvent être des composés chimiques ou des radiations, comme dans le cas de l’expérience de Morgan.
Les mutations qui n’affectent pas les cellules reproductives peuvent avoir différents impacts. Certaines sont silencieuses, sans effet, d’autres s’expriment sous certaines conditions (élévation de la température, etc…), mais certaines ont des conséquences très graves. En effet, la mutation est la première étape du cancer. En revanche, si elle affecte une cellule germinale (participant à la fécondation), elle est transmise à l’héritier. Elle peut elle aussi avoir un effet bénéfique, mais aussi délétère, voire létal. Les mutations favorables, bien que rares auront tendance à s’accumuler et ainsi à participer à l’évolution de l’espèce.
Sources:
Principes de l'algorithmie génétique
1) Méthodologie principale
Les algorithmes génétiques sont des algorithmes d'optimisation regroupant des méthodes de recherche de solutions approchées, dérivées de la génétique et de processus naturels tels que les croisements, les sélections, la reproduction ou encore la mutation d'espèces. L'algorithme génétique reproduit ce modèle d'évolution, composé de différentes étapes, et l'applique à un domaine de recherche défini pour trouver un solution à un problème donné.
Le but de ce type d'algorithme est de faire évoluer une population afin de l'améliorer. Il s'agit plus théoriquement, à partir de la création de la population initiale, de faire évoluer la fonction de sélection des individus de la population en réitérant plusieurs cycles de l'algorithme jusqu’à trouver le ou les extremum de la fonction, c'est-à-dire la solution ou l'ensemble de solutions optimales.
L'algorithme génétique dispose des cinq étapes suivantes :
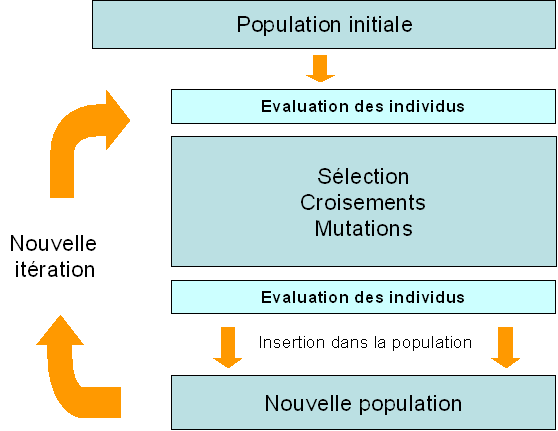
1) La création de la population
Le processus d'un algorithme génétique s’exécute à partir d'une population initiale à faire évoluer. La première étape est la mise en place d'un « principe de codage de l'élément ». « Cette étape associe à chacun des points de l'espace (éléments de population), une structure de données », c'est-à-dire la définition d'une forme générique de la solution comportant une structure de données afin que tous les éléments crées soient du modèle d'une solution potentielle. Cela nécessite d'avoir auparavant interprété et modélisé mathématiquement le problème traité. La qualité du codage des données détermine le succès des algorithmes génétiques.
Le procédé de création des individus de la population est arbitraire, il doit être capable de produire une population d'individus non homogène qui établie une base pour les générations suivantes. Le choix de la population est déterministe car sa pertinence influe sur la capacité de l'algorithme à converger plus ou moins rapidement vers l'optimum global. Lorsqu'on est confronté à un problème dont on ne connaît rien, il est primordial que la population initiale soit répartie sur l'ensemble du domaine de recherche.
2) Evaluation des individus
Une fois la population initiale déterminée, l'ensemble des individus de la population est évalué grâce à une fonction dite « fitness » ou fonction d'évaluation dans le but de sélectionner les individus qui seront les meilleurs parents pour la génération future. Cette fonction permet d'attribuer à chaque individu, un « degré d'élitisme » (ou degré de fitness) à maximiser selon la qualité de l'individu par rapport au problème posé. Un élément de population qui viole une contrainte se verra attribuer une mauvaise fitness et aura une probabilité forte d'être éliminé par le processus de sélection. Cette méthode permet de s'assurer que les individus performants seront conservés, alors que les individus peu adaptés seront progressivement éliminés de la population.
3) Sélection, croisements et mutations
L'étape suivante est la sélection. Il s'agit de la sélection des individus qui vont participer à l'amélioration de la population, c'est-à-dire la sélection d'individus qui deviendront « parents » en subissant l'action des opérateurs de croisement et de mutation créant de nouveaux individus « enfants » qui seront des meilleures solutions à notre problème. La méthode de sélection est arbitraire, elle peut être aléatoire ou basé sur la qualité des individus évalués grâce à la fonction fitness. Un exemple de méthode de sélection est la roulette ou « roulette wheel » c'est une méthode de sélection proportionnelle au degré de fitness. On associe à chacun des éléments de la population un secteur de la roue dont l'angle est proportionnel à la qualité (degré de fitness) de l'élément. On fait tourner la roue et on obtient un individu. « Les tirages des individus sont alors pondérés par leur qualité. Ainsi, les meilleurs individus ont plus de chance d'être croisés et de participer à l'amélioration de notre population. » Il existe d'autres méthodes de sélection telles que la sélection par rang ou encore la sélection par tournoi plus ou moins efficaces selon le problème à traiter.
Le croisement ou cross-over est le mécanisme de création de nouveaux individus en simulant le mécanisme de reproduction. Cet opérateur permet « la recombinaison des informations présentes dans le patrimoine génétique de la population ». Il manipule les chromosomes ou ensembles de paramètres de deux éléments parents en les copiant et les recombinant pour générer deux descendants possédant les caractéristiques issues des deux parents. Un ou plusieurs point de croisements sont placés au hasard sur les chaînes de paramètres des individus parents qui sont donc séparées en segments. Chaque segment du parent 1 est ensuite échangé avec son équivalent du parent 2 afin d'obtenir deux chaînes recomposées constituant les individus enfants. Voir figure ci-dessous qui représente un crossover avec un seul point de croisement.

La probabilité de croisement représente la fréquence à laquelle les croisements sont appliqués. Elle croit selon le nombre de points de croisements. Ainsi plus il y a de points de croisements, plus la probabilité de croisements est élevée et donc la population à de diversité.
La mutation est une autre manière modifier la population en créant de nouveaux éléments. Elle consiste en la modification d'un ou plusieurs paramètres de la chaîne en choisissant une valeur de remplacement aléatoire. Il en résulte la création d'un nouvel individu différent de l'élément initial selon un taux de mutation généralement faible (entre 0,5 % et 1%) c'est-à-dire que cet opérateur est appliqué sur un nombre limité d'individus et n'entraîne que quelques modifications sur ces individus. En général, on choisit de ne faire muter qu'un gêne ou paramètre de la structure de données de l'individu. Cela permet de garder une certaine diversité dans la population d’empêcher une convergence prématurée vers l'extremum globale et une possible dérive génétique.
4) Production d'une nouvelle population
Une fois les nouveaux individus crées, il faut à présent déterminer la nouvelle population en sélectionnant les individus parmi la population initiale et les nouveaux individus, qui feront partie de la prochaine génération. Une nouvelle étape de sélection est ainsi nécessaire à l'aide du même type de mécanismes de sélection vus précédemment, il aussi possible de reprendre une étape d'évaluation. Pour un souci de diversité et pour empêcher tout problème de convergence prématurée, il est important que la nouvelle population possède un nombre égal ou plus élevé d'individus que la population initiale. En effet, un nombre d'individus trop petit pour les nouvelle génération pourrait emmener à la disparition de la population et un nombre trop grand pourrait entraîner un temps de traitement infini.
5) Réitération du processus
La nouvelle population est enfin obtenue, le processus doit être réitéré un certain nombre de fois jusqu’à créer un nombre significatif de générations et obtenir une population contenant une ou des solutions convenables. Le nombre maximum de générations est arbitraire. Une fois atteint, la population finale possédera les meilleurs solutions que l'algorithme peut générer mais il n'y a pas de garantie que la solution optimale au problème s'y trouve. C'est la raison pour laquelle les algorithmes génétiques sont des approches incomplètes.
Sources:
2) Méthodologie mathématique
De manière plus concrète, un algorithme génétique se traduit de la manière suivante :
Il consiste en l’exploration d’un espace de configuration de n points solutions potentielles à un problème P. Chaque point se traduit par un chromosome codé par une chaine de l symboles d’un alphabet fini – généralement binaire.
Un chromosome est défini par une succession de gènes eux même définis par deux paramètres : la position dans la chaine dit locus et la valeur dit allèle. Ainsi un chromosome de huit symboles binaires peut être représenté comme ceci :

Le but de l’algorithme va être de faire évoluer selon uns fonction f positive, dit adaptative, une population aléatoire de n individu.
La fonction f restant à être déterminée suivant le problème de manière judicieuse.
Pour faire évoluer cette population de n chromosomes, on applique à l’ensemble des individus trois opérations :
L’opération dite de sélection, où l’on applique à chaque individu la fonction f pour en déterminer le taux d’adaptabilité, seuls les individus les plus adaptés pourront accéder à la « reproduction ».
L’opération dite de crossover, de probabilité d’exécution pc – l’opération ayant lieu pour chaque individu sélectionné si pc=1 et pour aucun si pc =0. Le crossover consiste à sélectionner deux individus particulièrement bien adaptés ; i.e. avec un coefficient d’adaptation, calculé selon f, supérieur aux autres et de les croiser selon un point de césure placé de manière aléatoire dans la chaine. Ainsi deux nouveaux individus sont créés. Par exemple :
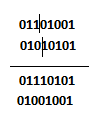
L’opération dite de mutation, de probabilité pm – l’opération ayant lieu pour chaque individu sélectionné si pm=1 et pour aucun si pm =0. L’opération consiste à changer de manière aléatoire l’allèle (valeur) d’un ou plusieurs gènes. Cette opération, généralement de probabilité très faible – de l’ordre de 0,001%- permet d’explorer un nouvel espace de solutions inaccessible par le crossover. Ainsi :
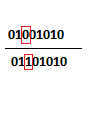
Enfin une fois le processus terminé, on calcule à nouveau le coefficient d’adaptabilité selon f des nouveaux chromosomes ainsi créés. Si leur coefficient est dans la partie supérieure de la population, ils seront intégrés à l’ensemble sujet à la « reproduction ». Puis on recommence jusqu’à trouver une solution correcte à P.
Exemple
Pour illustrer les opérations génétiques décrites auparavant, nous allons développer un exemple :
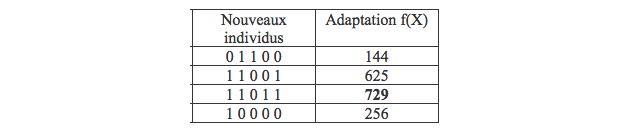
Nous prenons une population initiale, créée de manière aléatoire, composée de 4 individus (n=4) d'une longueur de 5 bits (l=5). Le but ici est de maximiser la fonction f qui pour un X binaire de 5 bits, donne un entier positif.
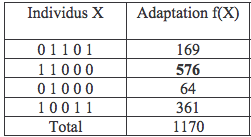
Dans notre cas, la fonction d’adaptation qui reflètera la probabilité que possède un individu de se reproduire sera aussi la fonction f, rapportée à la population entière (l’élément « 11000 » est ici celui qui est le plus apte à la reproduction).
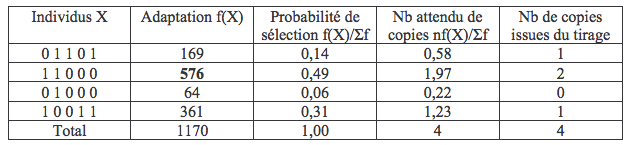
A l’issue du tirage au sort, les individus sélectionnés sont: un individu 1, deux individus 2, un individu 4 et pas d’individu 3. Nous allons donc passer à la phase de croisement dont les paramètres (appariement et position du crossover) sont établis aléatoirement. Pour simplifier les choses, nous prendrons une probabilité de mutation très faible (pm = 0,001), ce qui n’aura pour effet de ne pas avoir d’incidence sur les résultats.
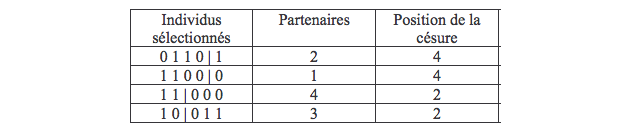
Il en résulte une nouvelle population plus performante sur le plan d’adaptation du meilleur individu (759 contre 576) comme sur le plan de l’adaptation moyenne (438,5 contre 292,5):
3) Notion de schème
On comprend assez facilement qu’un algorithme génétique est très dépendant de la population de départ choisie. Cette dernière, pour être performante doit respecter certain critères. Pour bien comprendre ces critères, il est important d’assimiler la notion de schème.
Soit l’alphabet fini A= {a1, a2, …, ak} où k est un entier positif, sur lequel est construit un ensemble de chromosomes de longueur l. On définit l’alphabet A+= {a1, a2, …, ak, *} ou * représente n’importe quelle élément de A, * est dit symbole indiffèrent. On appellera schème l’ensemble des éléments de longueur l construit sur A+. Ainsi, pour l = 7, le schème H 10*001* représente :

Un schème peut être considéré comme un ensemble de chromosomes respectant un certain nombre de similarités (ici 5). Un schème est défini par deux autres grandeurs :
L’ordre, noté o(H), est le nombre de gènes de H instanciés. Ainsi pour H = 10*001*, o(H)=5.
La longueur utile, noté δ(H), est la distance entre le premier et dernier gène instanciés. Ainsi pour H = 10*001*, δ(H)=5
On peut à présent définir la loi d’évolution d’un schème au cours du temps.
Soit m(H, t) le nombre d’exemplaires d’un schème H à l’instant t, on définit m(H, t+1) par :
m(H, t+1) = m(H, t)*f(H)/fmoy (1)
Ou f(H)/fmoy représente l’adaptation moyenne des individus porteurs du schème sur l’adaptation moyenne de la population toute entière. Donc en théorie si je possède une population de huit individus d’un taux moyen d’adaptation de 0,2, comportant quatre chromosomes porteurs d’un schème spécifique d’adaptation 0,4 on doit obtenir après calcul du taux d’adaptation une population porteuse du schème de huit, soit la totalité. On comprend bien ici qu’un chromosome porteur d’un schème avec un bon taux d’adaptation par rapport au reste de la population aura une très forte croissante.
La seconde opération qui est effectuée est un crossover de probabilité pc. Or un crossover risque de détruire le schème. On définit donc la probabilité de destruction du schème par crossover par :
pc*δ(H)/l-1
L’équation (1) devient alors :
m(H,t+1) = m(H,t)*f(H)/fmoy*[1-pc*δ(H)/l-1] (2)
Il apparait clairement ici qu’un schème de longueur utile faible par rapport de sa longueur totale sera plus robuste.
Enfin la dernière opération, la mutation de probabilité pm, induit également un risque de destruction pour le schème H. On définit la probabilité de survie de H après mutation par : (1-pm)^o(H), en considérant pm << 1 on en déduit que (2) devient :
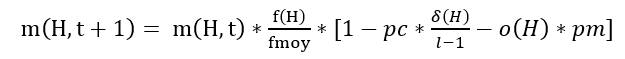
On comprend ici qu’un schème avec un ordre faible aura plus de chance de survivre à la mutation.
On appellera un schème « brique élémentaire » ssi
- δ(H) est court, car peu sensible au crossover
- o(H) d’ordre faible, car peu sensible à la mutation
- f(H)/fmoy élevé, impliquant un fort taux de duplication.
Ainsi toute la problématique et la difficulté d’un algorithme génétique sera de trouver un codage et une fonction d’adaptation qui permet l’utilisation de tels schèmes. Le risque étant sinon de ne jamais trouver une solution satisfaisante.
Note
m(H, t) n’est qu’une estimation du nombre d’individus porteurs du schème puisque sujet à des mécanismes probabilistes.
4) Le codage
On a pu voir dans l’exemple détaillé précédemment, que le codage choisi pour représenter les individus est le binaire. En effet, c’est une option judicieuse dans nombre de cas :
- pour exprimer un entier, ex: 18 <=> 1 0010
- pour exprimer un nombre décimal, ex: 0,69 <=> 1011000 (avec : 1*1/2+ 1*1/8+ 1/16 ≈ 0,69)
- pour représenter un ensemble de vecteurs, ex: (24, 5) <=> 1100000101
Pour s’assurer de sa pertinence il faut le comparer à d’autres types de codages comme par exemple les symboles alphabétiques :
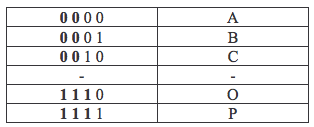
Pour éventuellement situer leur place dans l’alphabet, il est évident qu’il est plus facile de comparer 2 nombres binaires (0001 > 0010) que de comparer deux lettres telles que B et C.
Applications
C’est parce qu’il s’inspire de mécanismes naturels et biologiques (tels que la sélection naturelle) que l’algorithme génétique trouve son utilité dans des applications liées à l’humain. On en trouve donc dans des domaines associés au corps humain, comme la construction d’un réseau de neurones (l’AG est ici utile pour calculer le poids du réseau de neurones), ou encore dans le champ des robots humanoïdes. C’est le cas de Sony, avec son robot Aibo qui a utilisé ce type d’algorithme dit évolutionniste, afin d’optimiser son contrôleur de marche. En effet, lors des premiers tests, Aibo tombe fréquemment. Puis au fil des générations, ses mouvements se précisent et sa démarche s’en trouve améliorée. Encore une fois, il est possible de faire le parallèle entre cet apprentissage de la marche chez ce robot et celui de l’humain.
L’algorithme génétique est tout aussi performant dans le rayon du « data mining » ou exploration des données. C’est une extraction de connaissances de données qui consiste à récupérer une connaissance spécifique à partir d’une masse importante d’éléments (big data), et ce de manière automatique. Ses applications dans le monde de l’entreprise sont variées : maintenance préventive, détection de fraude ou encore optimisation de sites web ainsi que tout ce qui peut toucher à l’informatique décisionnelle. L’avantage de l’algorithme génétique dans ces cas est son approche itérative : il suffit de lui fournir un espace de recherche ainsi qu’un un critère d’efficacité ce qui est peu contraignant.
Il est donc possible de diviser l’utilisation des algorithmes génétiques en deux principales sections:
- Dans la représentation de l’apprentissage, avec des processus adaptatifs comme le robot Aibo (pouvant également servir dans l’univers de l’économie)
- Comme outil de d’optimisation et de prévision, au service du domaine de professionnel.
Aujourd’hui les algorithmes génétiques ne sont plus vraiment au gout du jour (Cette approche était particulièrement appréciée entre les années 2000 – 2005). Cependant on le retrouve couplé avec d’autre approche, notamment dans les systèmes de neurones artificiels.
Critiques des différents algorithmes
Quels sont les avantages et les inconvénients de ces approches? Nous traiterons les cas des algorithmes non déterministes et incomplets, et nous verrons que le paramètrage est très important.
1) Algorithme non déterministe et algorithme incomplet
Les algorithmes génétiques sont des algorithmes non déterministes et incomplets, ce qui amène à des limites dans les domaines de recherches ou la solution doit être optimale.
a) Algorithme non déterministe
Un algorithme non déterministe est un algorithme qui, pour la même population de départ, peut amener à différentes solutions pour plusieurs répétitions de l’algorithme. Particulièrement, dans le cas des algorithmes génétiques, les heuristiques de sélections des individus, c’est à dire les fonctions de sélections, ont un impact important. En effet, pour plusieurs passages, les mêmes individus ne seront pas forcément sélectionnées ce qui entraine par conséquence l’apparition de différents individus solutions.
b) Algorithme incomplet
Un algorithme incomplet est un algorithme qui ne garantit pas l’unicité d’une solution. En définitive, on n’est pas sur d’envisager toutes les solutions du problème. L’algorithme génétique ne garantit pas que l’on ait la meilleure solution, ou bien si il n’arrive pas à déterminer de solution, que le problème est insolvable.
2) Une grande importance du paramétrage
Les trois paramètres, sélection, mutation et croisement n’ont pas le même impact sur la résolution. Bien que cela réfère aussi à des problèmes liés à la modélisation du problème, on trouve certaines limites propres à des facteurs tels que la mutation ou les croisements. L’impact du paramétrage dépend aussi grandement du problème. La nécessite de devoir dans certains cas effectuer plusieurs essais pour affiner les paramètres de manière empirique nuit à l’efficacité de l’algorithme.
a) Problématique liée au paramètre de sélection
Le paramètre de sélection a un impact sur la convergence du fait qu’il est celui qui est modulable. Un des problèmes que l’on peut rencontrer avec la fonction de sélection est le problème de dominance d’un individu. Dans le cas d’optima locaux, la méthode classique peut avoir pour effet de faire converger la population vers un certain type d’individu, au dépend d’autres individus plus intéressant pour la résolution mais trop éloignés.
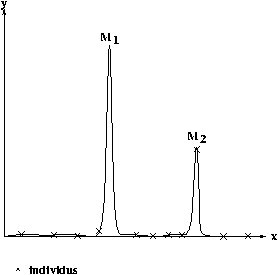
Ce problème peut cependant être pallié en utilisant différentes méthodes de sélections différentes de la méthode classique. C’est l’exploration de nouveaux espaces de solutions, avec par exemple la méthode de sélection par tournoi.
b) Problématique liée au paramètre de mutation
Le paramètre de mutation est indépendant du problème. Selon le problème rencontré, il va être plus ou moins adapté. Dans le cas d’une faible population, la mutation aura plus d’impact que dans le cas d’une forte population. Ca peut être une limite si l’espace de recherche est trop grand.
c) Problématique liée au paramètre de croisement
Comme pour le paramètre de mutation, ce paramètre ne peut pas être rendu dépendant à proprement parler du problème, puisque il est le même dans tous les cas d’études.
Le problème des croisements entre deux individus peut être biaisé si le codage des chromosomes implique que certains gènes sont mal positionnés. Si tous les éléments sont dans le même espace, l’opérateur de croisement n’est pas vraiment efficace.
Par exemple, si deux gènes importants g1 et g2 sont codés pour un premier chromosome sur les bits 1 et 8, et pour un deuxième chromosome sur les bits 1 et 2. Le croisement pour le premier chromosome s’opère facilement alors que pour le deuxième le croisement a peu de chance d’être représenté dans la population.
3) Impact de la modélisation du problème sur la résolution
Bien que le fonctionnement des algorithmes génétiques soit toujours le même, une connaissance minimum du problème est nécessaire pour rendre l’algorithme fonctionnel. Le codage, la construction de l’espace de solution et le choix de la fonction de fitness doivent être adaptés aux spécificités du problème.
a) Problématique liée à la fonction fitness
La fonction fitness, ou fonction d’évaluation n’est pas une méthode à proprement parlé lié aux algorithmes génétiques. Elle est définie en fonction du problème, et sa complexité peut donc varier en conséquence.
Dans le cas d’une fonction d’évaluation constante au cours du temps, le problème est que la fonction ne garantit pas forcément son efficacité au cours du temps. Ca peut être un problème pour la convergence de la solution. Cela dépend du problème, et c’est pour cela que la fonction d’évaluation est avant tout liée à un travail de modélisation.
On peut dans le même sens utilisé des fonctions d’évaluations très puissantes. Par exemple, on peut utiliser deux fonctions d’évaluations. De même, il est possible d’avoir une fonction qui évolue au cours du temps. Cependant, dans le cas d’un espace de recherche important, si on a une complexité trop grande, le rapport coût/performance n’est pas intéressant.
b) Codage du problème
Lors de la modélisation du problème, il est important de réfléchir à un codage pertinent des différentes propriétés. Un mauvais codage ne permettra pas d’identifier certaines solutions. Or, il n’est pas toujours facile d’identifier les bonnes propriétés lors du codage d’un problème. De plus, la fonction de décodage nuit à la performance de l’algorithme.
c) Construction de l’espace de solution
Pour certains problèmes, on ne sait pas forcément quelle taille de population choisir au départ. Dans le cas ou une grande population de départ est nécessaire, ca limite l’efficacité de l’algorithme.
Sources:
Bibliographie
A classer par ordre alphabétique de référence
as2000: Alexandre Saidi, 2010: Titre, Revue, Editeurbm2014: Bruno Mascret, 2014: Titre, Revue, Editeur